投影和相机

介于投影和相机比较复杂，由于个人能力有限，怕误导读者。因此这里引用LibGDX官方网站的一篇博客。该博客详细讲解了正交投影和透视投影以及LibGDX的正交投影相机和透视投影相机的使用方法。

(下面是本人翻译的中文版，由于个人能力有限，如有错误请阅读原文：http://www.badlogicgames.com/wordpress/?p=1550%E3%80%82)

New Camera Classes in libgdx

首先，相机是什么呢？场景中的相机不应当是下面这个样子么：

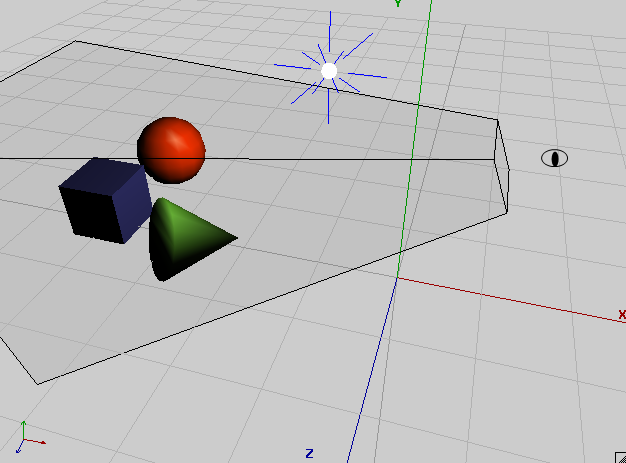
定义相机需要一个3D空间的位置(position)向量、一个定义方向(direction)的单位向量和一个表示向上(up)的单位向量。向上向量可以想象为一个从头顶指向天空的箭头。当你左右倾斜脑袋时，你是否可以想象到该向量的方向是如何变化的？结合方向向量和向上向量，我们便可以告知OpenGL相机在空间的姿态。位置向量可以告知OpenGL相机在3D空间的具体位置。

位置和姿态仅仅是一部分比较难理解的内容。第二个比较重要的概念就是相机的视锥(view frustum)。在上面的截图中，我们可以看到一个被切掉头部(眼睛的位置)的金字塔。该金字塔就称为视锥。位于视锥内部的所有物体都可以显示到屏幕上。视锥的范围由6个切面组成，分别是：near、far、left、right、top和bottom。由于上面截图仅仅显示了视锥的一边，因此我们只能看到三个切面。near切面扮演着一个特殊的角色：你可以将它想象成用于显示相机所拍摄的图片的平面。在此过程中，将一个3D空间的点转换为到2D切面的过程就称之为投影(projection)。一般来讲，我们会涉及到两种投影：正交投影(Orthographic)和透视投影(Perspective)。

大多数情况下，正交投影都应用于2D场景。在正交投影中，无论一个对象距离相机有多远，它投影在屏幕上的尺寸总是相同的。透视投影一般用于模拟真实世界：距离眼睛较远的物体看起来更小。

有趣的是，我们为相机定义的各种属性仅仅是为了修改视锥的形状。透视投影的视锥就是上面截图所展示的金字塔形状。然而，正交投影的视锥就像一个盒子，其投影的原理非常简单：首先，从对象的每一个点沿着相机的方向绘制一条互相平行直线，然后计算该直线在near切面上击中的位置（虽然这个描述并不完全正确，但是可以帮助我们理解最基本的原理）。下面截图解释了这两种投影的区别：

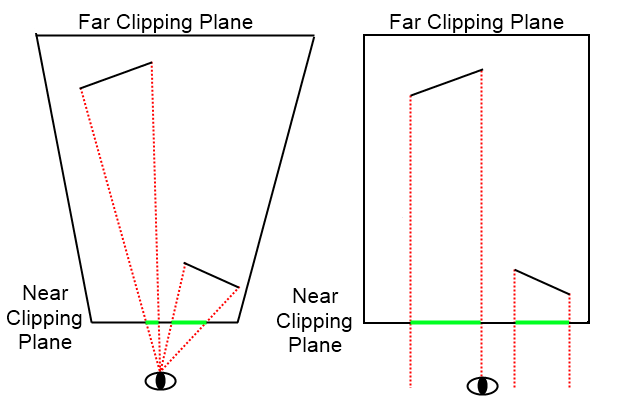
现在，你是否明白为什么经过透视投影之后对象变得更小了？或者说为什么经过正交投影之后对象的尺寸没有发生改变？两种投影唯一的区别就是视锥的形状不同。在OpenGL中，无论你是使用SpriteBatch渲染对象还是绘制一行文本，我们的工作场景永远都是3D空间。只不过在使用正交投影相机时，我们假装z轴不存在而已。下面截图展示了一个位3D空间的2D精灵对象：

所以，忘记2D与3D之间的区别吧！他们之间没有什么不同。从现在起，下面截图所展示的盒状体就是使用没有任何材质信息的SpriteBatch对象渲染的视锥形状：

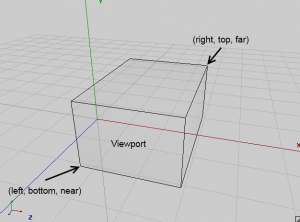
它仅仅是一个让人讨厌的盒子。我们所需要做的就是将精灵对象平移至X/Y切面，忽略z轴的存在，其实我们只是假象工作在一个真实的2D空间。

透视投影相机利用两个属性定义了投影过程：视域(filed of view)和宽高比(aspect ratio)。视域就是一个定义了视锥如何打开的角度：

宽高比表示视口(viewport)的宽度和高度的比率。视口定义了相机“拍摄”的图片所渲染的矩形区域。因此，如果一个设备的屏幕尺寸是480×320像素，则该屏幕的宽高比等于480/320。

正交投影相机的投影仅由它的视口尺寸定义。我们可以从上面的截图验证这一点（正交投影的视锥是一个盒状体）。

接下来介绍LibGDX的相机是如何工作的。这里我们将涉及到三个类：基础类Camera、正交投影相机类OrthographicCamera和透射投影相机类PerspectiveCamera。后面两个类都继承于Camera类，所以它们也共享了同样的成员和属性。首先让我们看一下Camera类：

public abstract class Camera {
  public final Vector3 position = new Vector3();
  public final Vector3 direction = new Vector3(0, 0, -1);
  public final Vector3 up = new Vector(0, 1, 0);
  ...

前三个公共成员分别表示相机的位置向量，方向向量和向上向量。每个成员都被初始化为标准值，所谓的标准值表示相机位于原点、观察方向指向z轴的负半轴、向上向量指向y轴上方。我们可以通过访问并修改这些成员来操纵相机的姿态。

  public final Matrix4 projection = new Matrix4();
  public final Matrix4 view = new Matrix4();
  public final Matrix4 combined = new Matrix4();
  public final Matrix4 invProjectionView = new Matrix4();

上面包含四个矩阵。只有当使用OpenGL ES 2.0时我们才会关心它们。前两个分别是投影矩阵和视图矩阵。第三个表示前两个矩阵的乘积并转置获得的联合矩阵。该矩阵通常用于采集信息等任务。正如我所想，通常你不会乐意去接触这些矩阵的。

  public float near = 1;
  public float far = 100;
  public float viewportWidth = 0;
  public float viewportHeight = 0;

接下来包含四个浮点型变量，其中near和far分别定义了near切面和far切面与相机之间的距离，viewportWidth和viewportHeight定义了视口的尺寸。near切面与far切面必须满足0 ≤ near < far。虽然我们可以使用一个setter方法断言上述条件，但是我最终决定暴露这些私有的成员，不使用任何安全措施。默认的near切面与相机的距离等于1单位，对于正交投影相机，通常应该设置为0（正交投影相机会在构造方法内自动完成这一任务）。视口的宽高定义了透视投影相机的宽高比以及正交投影的盒状视锥。

  public final Frustum frustum = new Frustum();

最后一个成员是Frustum类。该类包含了组成相机视锥的6个剪切面。Frustum一般被当做选择器使用：检查一个对象是否位于视锥内部。如果不在，我们就没有必要渲染它。Frustum类提供了大量用于检查BoundingBox、Sphere或Point是否位于视锥内部的方法，从而决定对象是否可见。关于这一点请看javadocs。

  public abstract void update();

接下来我们介绍一些非常有用的方法。update()方法用于重新计算并更新相机内部的矩阵。我们应该在每次修改相机的属性之后调用该方法，例如postion或者near/far剪切面等等。

  public void lookAt(float x, float y, float z);
  public void rotate(float angle, float axisX, float axisY, float axisZ);
  public void translate(float x, float y, float z);

上面列举了一系列方法，这些方法允许我们设置相机的观察方向(direction)，围绕任意轴旋转任意角度，平移指定增量位移。通过这些简单的方法，我们可以直接操纵相机的位置position/方向direction和向上up向量。

public void unproject(Vector3 vec);
public void project(Vector3 vec);
public Ray getPickRay(float x, float y);

最后，我们列举了几个应用于高级功能的方法。unproject()方法可以将一个位于窗口坐标系(或成为屏幕坐标系)的点转为3D空间的坐标。参数vec的x和y传递触摸点的坐标即可，而z需要传递一个位于0到1之间的浮点数，0表示在near切面生成一个点，1表示在far切面生成一个点。project()方法刚好做的是相反的事情：将3D空间中的一个点转化为2D屏幕上的一个点。getPickRay()方法返回一个用于ray picking技术的Ray对象。